浅析主流排序算法

排序算法作为计算机科学中的基础课题，其重要性不言而喻。它们在日常开发、数据分析、机器学习等诸多领域都有着广泛的应用。

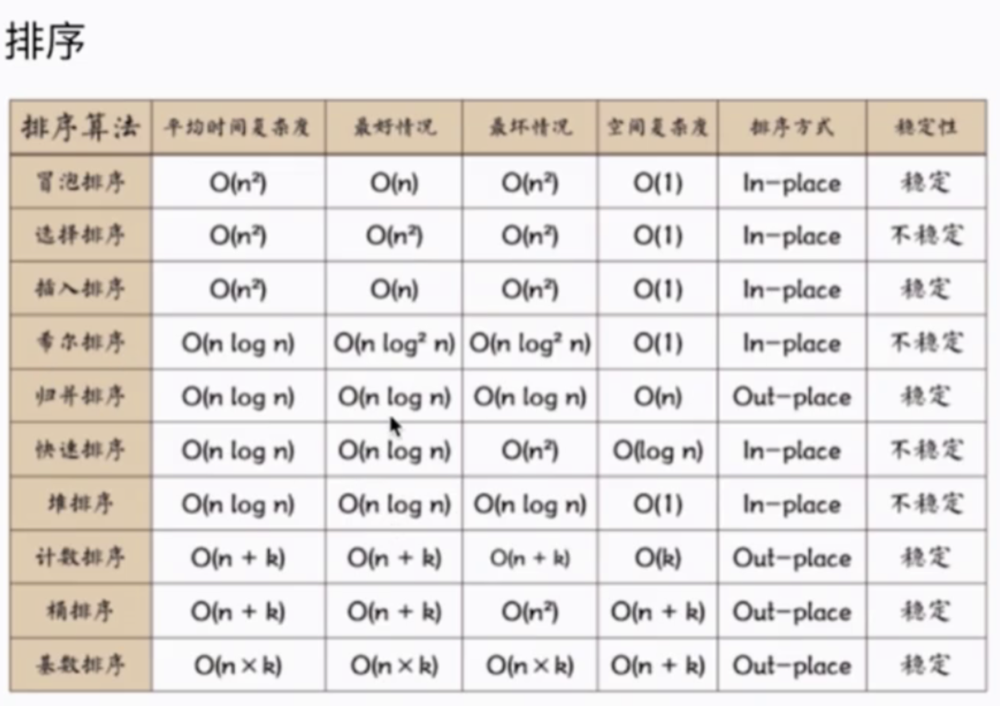
一、排序算法分析

1 执行效率

• 最好时间复杂度、最坏时间复杂度和平均时间复杂度
• 时间复杂度的系数、常数和低价
• 比较次数和交换（或移动）次数

2 内存消耗

• 空间复杂度
• 原地排序和非原地排序（原数据存储）

3 稳定性

• 稳定排序算法：值相等的元素，排序后先后顺序不变
• 不稳定排序算法：值相等的元素，排序后先后顺序改变

二、排序算法

1. O(n^2)排序

一般使用双循环。

1.1 冒泡排序（bubble sort） O(n^2)

• 空间复杂度 O(1)
• 稳定排序
• 最好时间复杂度：数组已经有序时，O(n)
• 最坏时间复杂度：数组倒序时，O(n^2)
• 平均时间复杂度：有序度，无序度，平均交换次数（有点复杂），O(n^2)

//冒泡排序:当一个数比后一个数大时，交换两者的位置，每遍历一次就把遍历范围内的最大数的排到遍历的末尾
//优化：当某次操作已经没有数据交换时，数组变为有序，退出后续遍历
function bubbleSort(nums) {
  let n = nums.length;
  if (n <= 1) return nums;
  for (let i = 0; i < n; i++) {
    let flag = false; //提前退出冒泡循环的标识位
    for (let j = 0; j < n - i - 1; j++) {
      //最大的数已经排到了数据末尾，所以每次循环都减去i
      if (nums[j] > nums[j + 1]) {
        //交换相邻的两个元素
        let tmp = nums[j];
        nums[j] = nums[j + 1];
        nums[j + 1] = tmp;
        flag = true;
      }
    }
    if (!flag) break; //没有数据交换，退出循环
  }

  return nums;
}

1.2 插入排序（insert sort）O(n^2)

• 已排序区间，未排序区间
• 查找合适的位置插入数据，从未排序的区间取元素，到已排序区间找到合适的位置插入
• 原地排序，空间复杂度 O(1)
• 稳定排序算法
• 最好时间复杂度：数组已经有序时，O(n)
• 最坏时间复杂度：数组倒序时，O(n^2)
• 平均时间复杂度：有序度，无序度，平均交换次数（有点复杂），O(n^2)

function insertSort(nums) {
  let n = nums.length;
  if (n <= 1) return nums;
  for (let i = 1; i < n; i++) {
    let value = nums[i];
    let j = i - 1;
    for (; j >= 0; j--) {
      //查找插入的位置
      if (nums[j] > value) {
        nums[j + 1] = nums[j]; //移动数据
      } else {
        break;
      }
    }
    nums[j + 1] = value;
  }
  return nums;
}

1.3 选择排序(select sort) O(n^2)

• 已排序区，未排序区
• 每次从未排序区中取最小的元素，放到已排序区间的末尾
• 原地排序，空间复杂度 O(1)
• 不是稳定排序算法
• 最好时间复杂度：数组已经有序时，O(n^2)
• 最坏时间复杂度：数组倒序时，O(n^2)
• 平均时间复杂度：有序度，无序度，平均交换次数（有点复杂），O(n^2)

function selectSort(nums) {
  let n = nums.length;
  if (n <= 1) return nums;

  for (let i = 0; i < n - 1; i++) {
    let minIndex = i;
    for (let j = i; j < n; j++) {
      //查找min
      if (nums[j] < nums[minIndex]) {
        minIndex = j;
      }
    }
    //交换元素
    let tmp = nums[i];
    nums[i] = nums[minIndex];
    nums[minIndex] = tmp;
  }

  return nums;
}

---

2. O(nlogn) 排序

分治算法思想，递归编程技巧。

2.1 归并排序 O(nlogn)

• 稳定排序算法
• 不是原地排序算法
• 最好时间复杂度：O(nlogn)
• 最坏时间复杂度：O(nlogn)
• 平均时间复杂度：O(nlogn)
• 空间复杂度 O(n+logn)，即 O(n)

递推公式：mergeSort(p,r) = mergeSort(mergeSort(p,q),mergeSort(q+1,r))

终止条件：p>=r，mergeSort(p,r)表示对下标 p 到 r 的数组进行归并排序

function mergeSort(nums) {
  let n = nums.length;
  if (n <= 1) return nums;

  let mid = Math.floor(n / 2);
  const left = nums.slice(0, mid);
  const right = nums.slice(mid);

  return merge(mergeSort(left), mergeSort(right));
}

//将两个有序的数组合并成一个
function merge(left, right) {
  let result = [];
  let i = 0;
  let j = 0;

  while (i < left.length && j < right.length) {
    if (left[i] < right[j]) {
      result.push(left[i]);
      i++;
    } else {
      result.push(right[j]);
      j++;
    }
  }

  //处理有剩余的数组
  while (i < left.length) {
    result.push(left[i]);
    i++;
  }

  while (j < right.length) {
    result.push(right[j]);
    j++;
  }

  return result;
}

2.2 快速排序 O(nlogn)

• 不是稳定排序算法
• 是原地排序算法
• 最好时间复杂度：O(nlogn)
• 最坏时间复杂度：O(n^2)
• 平均时间复杂度：O(nlogn)
• 空间复杂度 O(logn)
• 最坏空格复杂度 O(n)

递推公式：quickSort(p,r) = partition(p,r) + quickSort(p,q) +quickSort(q+1,r)

终止条件：p>=r

function quickSort(nums) {
  let n = nums.length;
  if (n <= 1) return nums;

  let mid = Math.floor(n / 2);
  const pivot = nums[mid];
  const smaller = [];
  const equal = [];
  const larger = [];

  for (let num of nums) {
    if (num < pivot) {
      smaller.push(num);
    } else if (num === pivot) {
      equal.push(num);
    } else {
      larger.push(num);
    }
  }

  return [...quickSort(smaller), ...equal, ...quickSort(larger)];
}

如何优化快速排序？

理想分区点：被分区点分开的两个小区间大小接近相等。

合理选择分区点：

• 三数取中法：取区间的首、中、尾三个数比较大小，取这三个数的中间值作为分区点。数组大可以用“五数取中“，”十数取中”
• 随机法：每次从要排序的区间中随机选择一个元素作为分区点。不能保证每次都是最好，但也不会每次都是最差。

3. O(n) 排序

线性排（linear sort），不是基于比较的排序算法

3.1 桶排序(bucket sort) O(n)

核心思想：先定义几个有序的“桶”，将要排序的数据分到这几个”桶“，对每个“桶”单独排序，再把每个桶的数据按照顺序依次取出，组成有序的序列。

桶排序的效果，取决于桶的大小和分布，不是所有情况下都是最优的。

//nums:[22,5,11,41,45,26,29,10,7,8,30,27,42,43,40]
//bucketSize:5
function bucketSort(nums, bucketSize) {
  if (nums.length <= 1) return nums;

  let min = 0; //5
  let max = 0; //46

  //确定最大和最小值
  for (let i = 1; i < nums.length; i++) {
    if (nums[i] < min) min = nums[i];
    else if (nums[i] > max) max = nums[i];
  }

  //创建桶
  let bucket = Array(bucketSize + 1).fill([]);

  //把数据分配到桶中
  for (let i = 0; i < nums.length; i++) {
    let bucketIndex = Math.floor(nums[i] / ((max - min) / bucketSize));
    bucket[bucketIndex].push(nums[i]);
  }

  //对每个桶进行排序，并将结果放进数组
  let res = [];
  for (let i = 0; i < bucket.length; i++) {
    let data = bucket[i].sort((a, b) => a - b);
    res = [...res, ...data];
  }
  return res;
}
let nums = [22, 5, 11, 41, 45, 26, 29, 10, 7, 8, 30, 27, 42, 43, 40];
console.log("原数组：", nums);
console.log("桶排序后：", bucketSort(nums, 5));

3.2 计数排序(counting sort) O(n)

是桶排序的一种特殊情况。桶的个数就是最大值 k。如果 k 远小于 k，则时间复杂度为 O(n)，k 很大则不适合使用计数排序。

• 时间复杂度 O(n+k)
• 适用于给非负整数排序

function countingSort(nums) {
  if (nums.length <= 1) return nums;

  //查到最大值
  let max = nums[0];
  for (let i = 1; i < nums.length; i++) {
    if (max < nums[i]) max = nums[i];
  }

  //申请一个计数数组c，下标范围是[0,max]
  let c = Array(max + 1).fill(0);
  //计算每个元素的个数，放入数组c
  for (let i = 0; i < nums.length; i++) {
    c[nums[i]]++;
  }

  //依次累加，每一项表示在排序后，小于和等于某数的个数
  for (let i = 1; i <= max; i++) {
    c[i] = c[i - 1] + c[i];
  }

  //数组r，存储排序后的结果
  let r = Array(nums.length);
  //从后往前遍历，为了保证排序算法的稳定性
  for (let i = nums.length - 1; i >= 0; --i) {
    let index = c[nums[i]] - 1;
    r[index] = nums[i];
    c[nums[i]]--;
  }

  return r;
}
const nums = [2, 5, 3, 0, 2, 3, 0, 3];
console.log("排序前：", nums);
console.log("排序后：", countingSort(nums));

3.3 基数排序(radix sort) O(n)

将数据按照每一位的值进行排序，从低位到高位依次排序，最终得到有序的结果。例如比较手机号，从最后第 11 位按照 0-9 排序。

//[123, 45, 67, 890, 12, 345, 678, 901]
function radixSort(nums) {
  if (nums.length <= 1) return nums;

  //查找最大值
  let max = nums[0];
  for (let i = 1; i < nums.length; i++) {
    if (max < nums[i]) max = nums[i];
  }

  //exp基数
  for (let exp = 1; Math.floor(max / exp) > 0; exp *= 10) {
    countingSort(nums, exp);
  }

  return nums;
}

function countingSort(nums, exp) {
  let count = Array(10).fill(0);
  //计算个数
  for (let i = 0; i < nums.length; i++) {
    const digit = Math.floor(nums[i] / exp) % 10;
    count[digit]++;
  }

  //累加
  for (let i = 1; i < 10; i++) {
    count[i] += count[i - 1];
  }

  let res = Array(nums.length);
  for (let i = nums.length - 1; i >= 0; i--) {
    const digit = Math.floor(nums[i] / exp) % 10;
    res[count[digit] - 1] = nums[i];
    count[digit]--;
  }

  for (let i = 0; i < nums.length; i++) {
    nums[i] = res[i];
  }
}

const nums = [123, 45, 67, 890, 12, 345, 678, 901];
console.log("排序前：", nums);
console.log("排序后：", radixSort(nums)); // 输出：[12, 45, 67, 123, 345, 678, 890, 901]

3.4 其他 O(n)的排序算法

• 堆排序
• “猴子”排序
• 睡眠排序
• “面条”排序