数据结构之二叉树
一、定义与结构
1.1 定义
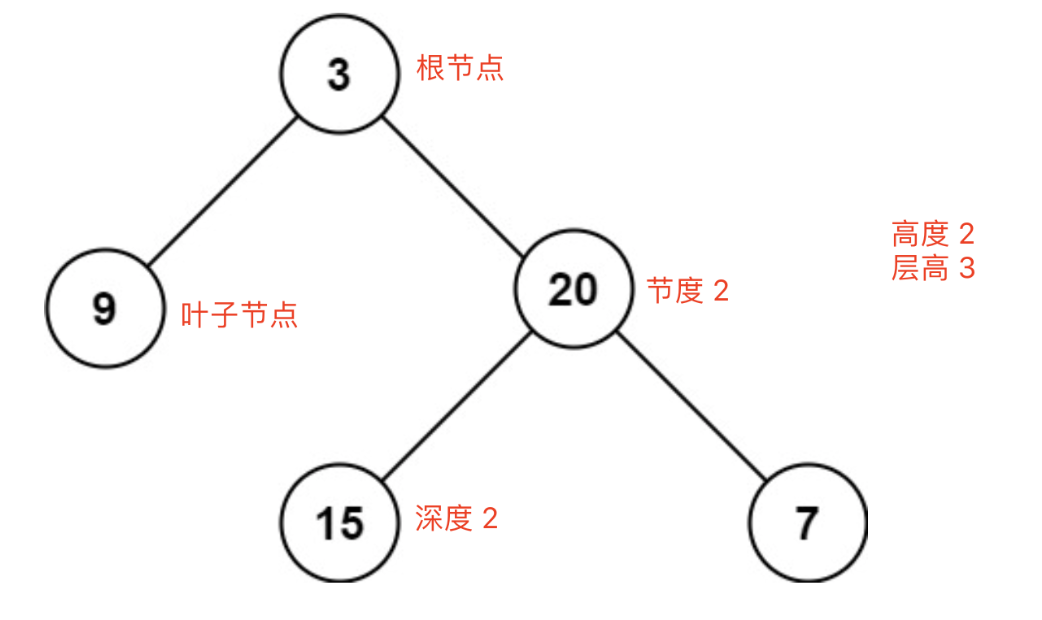
- 根节点:没有父节点的节点。
- 叶子节点:没有子节点的节点。
- 高度:节点到叶子节点的最长路径长度(边数),height。
- 深度:根节点到这个节点的路径长度(边数),depth。
- 层:节点的深度+1,level。
- 树的高度:根节点的高度。
- 节度点:节点的度是指一个节点拥有的子节点数目。在二叉树中,节点的最大度数为 2。
1.2 结构
- 二叉树是由 n(n≥0)个节点构成的有限集合。
- 每个节点最多包含两个子节点,分别称为左孩子(left child)和右孩子(right child)。
- 存在一种特殊的二叉树:空树(n=0),即没有任何节点的树。
- 根节点是没有父节点的特殊节点。
1.3 存储
基于指针(或引用)的链式存储:非完全二叉树
- 每个节点包含三个部分:数据域、左子节点指针和右子节点指针。
- 节点之间通过指针链接起来形成逻辑上的树结构,不受物理存储空间的限制。
- 优点:灵活,适合任意形态的二叉树(包括不平衡的二叉树),插入和删除操作无需移动其他节点,只需修改相关节点的指针即可。
- 缺点:额外的空间消耗用于存储指针,且访问效率取决于树的高度,最坏情况下退化成线性时间复杂度。
function TreeNode(val, left, right) {
this.val = val === undefined ? 0 : val;
this.left = left === undefined ? null : left;
this.right = right === undefined ? null : right;
}
const root = new TreeNode(3);
root.left = new TreeNode(9);
root.right = new TreeNode(20);
root.right.left = new TreeNode(15);
root.right.right = new TreeNode(7);
基于数组的顺序存储:完全二叉树
- 适用于完全二叉树或满二叉树。
- 使用一个连续的数组来存储二叉树的所有节点,数组中的索引与节点在完全二叉树中的层级和位置相对应。
- 对于节点下标 i,它的父节点 i/2,左子节点:2i,右子节点:2i+1
- 优点:存储空间利用率高,如果是一棵完全二叉树,那么空间几乎不浪费。
- 缺点:对非完全二叉树,会有大量空位,浪费存储空间;插入和删除操作可能需要移动大量元素以维持数组的完整性。
const root = [3, 9, null, null, 20, 15, 7];
二、常见类型
2.1 二叉搜索树
Binary Search Tree, BST。在二叉搜索树中,对于任意节点来说,其左子树中的所有节点的值都小于该节点的值,而右子树中的所有节点的值都大于该节点的值
- 在二叉搜索树中查找、插入和删除操作的时间复杂度在理想情况下可以达到 O(log n)
- 中序遍历二叉搜索树得到的结果是一个递增有序的序列
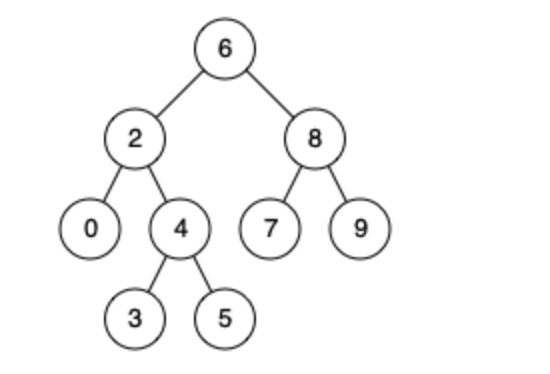
查找操作
先与根节点比较,相等则返回根节点的值,比根节点小,则查找左子树,比根节点大则查找右子树。
function search(root, p) {
let cur = root;
while (cur != null) {
if (p === cur.val) return cur;
else if (p < cur.val) cur = cur.left;
else cur = cur.right;
}
return null;
}
//递归写法
function search(root, p) {
if (!root || root.val === p) return root;
if (root.val > p) return search(root.left, p);
return search(root.right, p);
}
插入操作
插入数据比当前节点大,则往右子树查找为空的位置插入,假如比当前节点小,则往左子树查找为空的位置插入。
function insert(root, p) {
// root 为空,创建一个新的节点
if (!root) return new Node(p);
const cur = root;
while (cur) {
if (p > cur.val) {
// 如果右子节点为空,则插入新节点作为右子节点,并返回根节点
if (cur.right == null) {
cur.right = new Node(p);
break;
}
// 否则,移动到右子节点
cur = cur.right;
} else {
// 如果左子节点为空,则插入新节点作为左子节点,并返回根节点
if (cur.left == null) {
cur.left = new Node(p);
break;
}
// 否则,移动到左子节点
cur = cur.left;
}
}
return root;
}
//递归写法
function insert(root, p) {
if (!root) return new Node(p);
if (root.val > p) {
root.left = insert(root.left, p);
} else if (root.val < p) {
root.right = insert(root.right, p);
} else {
return root;
}
return root;
}
删除操作
- 删除的节点右两个子节点:查找要删除节点的右子树的最小节点,用最小节点的值替换要删除节点的值,并把原先指向最小节点的指针置为 null。
- 删除的节点有一个子节点:将要删除节点的父节点指向该子节点。
- 删除的节点没有子节点:将父节点指向要删除节点的指针置为 null。
/**
* 删除二叉搜索树中的指定节点
* @param {TreeNode} root - 二叉搜索树的根节点
* @param {number} p - 需要删除的节点的值
* @returns {TreeNode} - 删除操作后二叉搜索树的根节点
*/
function deleteNode(root, p) {
// 如果根节点为空,直接返回,表示树中没有要删除的节点
if (!root) return root;
// 初始化当前节点 cur 和其父节点 pp
let cur = root;
let pp = null; // pp 用于记录待删除节点的父节点
// 寻找待删除节点 p 及其父节点
while (cur && cur.val !== p) {
pp = cur;
if (p < cur.val) {
// 目标值小于当前节点值,向左子树继续查找
cur = cur.left;
} else {
// 目标值大于等于当前节点值,向右子树继续查找
cur = cur.right;
}
}
// 如果没有找到待删除的节点,直接返回原树
if (!cur) return root;
// case 1: 待删除节点有两个子节点
if (cur.left && cur.right) {
// 找到右子树的最小节点
let minP = findMin(cur.right);
// 用右子树最小节点的值替换待删除节点的值
cur.val = minP.val;
// 递归删除右子树中的最小节点
cur.right = deleteNode(cur.right, minP.val);
}
// case 2 & 3: 节点只有一个子节点或没有子节点
else {
// 找到待删除节点的直接子节点,可能是左子节点或右子节点,也可能是null
const child = cur.left !== null ? cur.left : cur.right;
// 删除节点是根节点且没有子节点,整个树变为空
if (pp === root && child === null) {
root = null;
}
// 更新父节点的指针,指向子节点或null
else if (pp.left === cur) {
pp.left = child;
} else {
pp.right = child;
}
}
// 返回删除操作后的树的根节点
return root;
}
/**
* 在以node为根的二叉树中寻找最小节点
* @param {TreeNode} node - 当前搜索的子树的根节点
* @returns {TreeNode} - 最小节点
*/
function findMin(node) {
// 不断向左走,直到没有左子节点为止,即找到了最小节点
while (node.left) {
node = node.left;
}
return node;
}
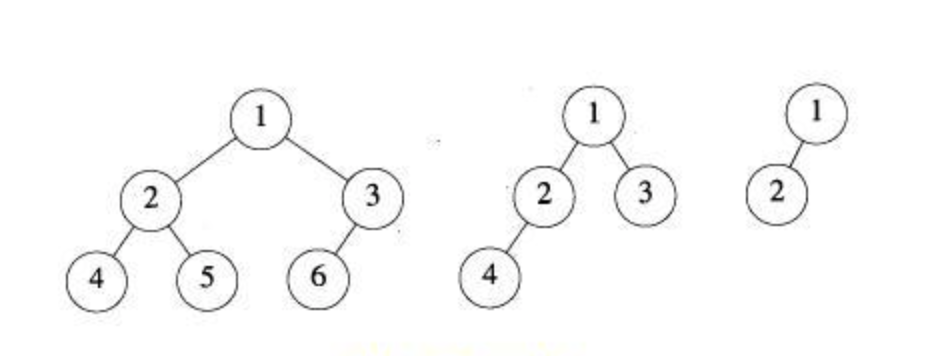
2.2 完全二叉树
Complete Binary Tree。除了最后一层外,每一层都被完全填满,并且所有结点都尽可能想左边靠拢。
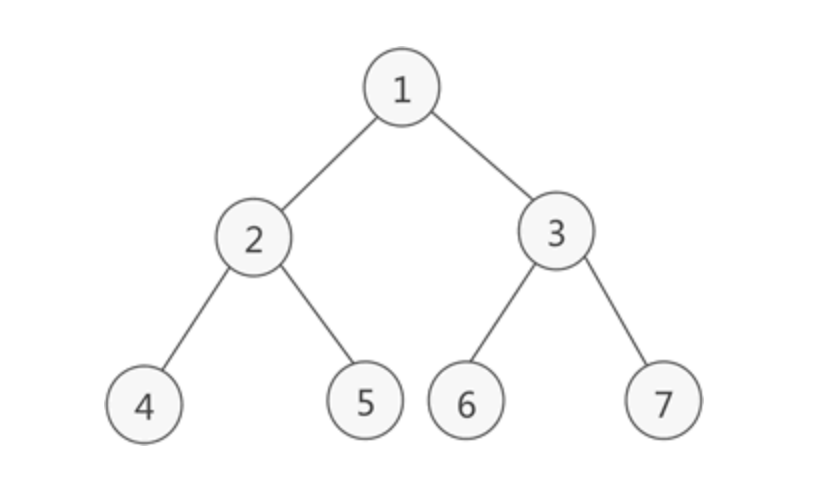
2.3 满二叉树
Full Binary Tree。所有层都被完全填满的二叉树,每个节点都有两个子节点或者没有子节点。
2.4 平衡二叉树
平衡二叉搜索树是一类特殊的二叉搜索树。左右两个子树的高度差不超过 1,保证了查找效率的平衡性,解决二叉树查找频繁插入、删除等动态更新导致的性能退化问题。
- 矮胖
- 完全二叉树、满二叉树是平衡二叉树,高度大于 log2n
- 红黑树、AVL 树、Treap(树堆)、Splay Tree(伸展树)
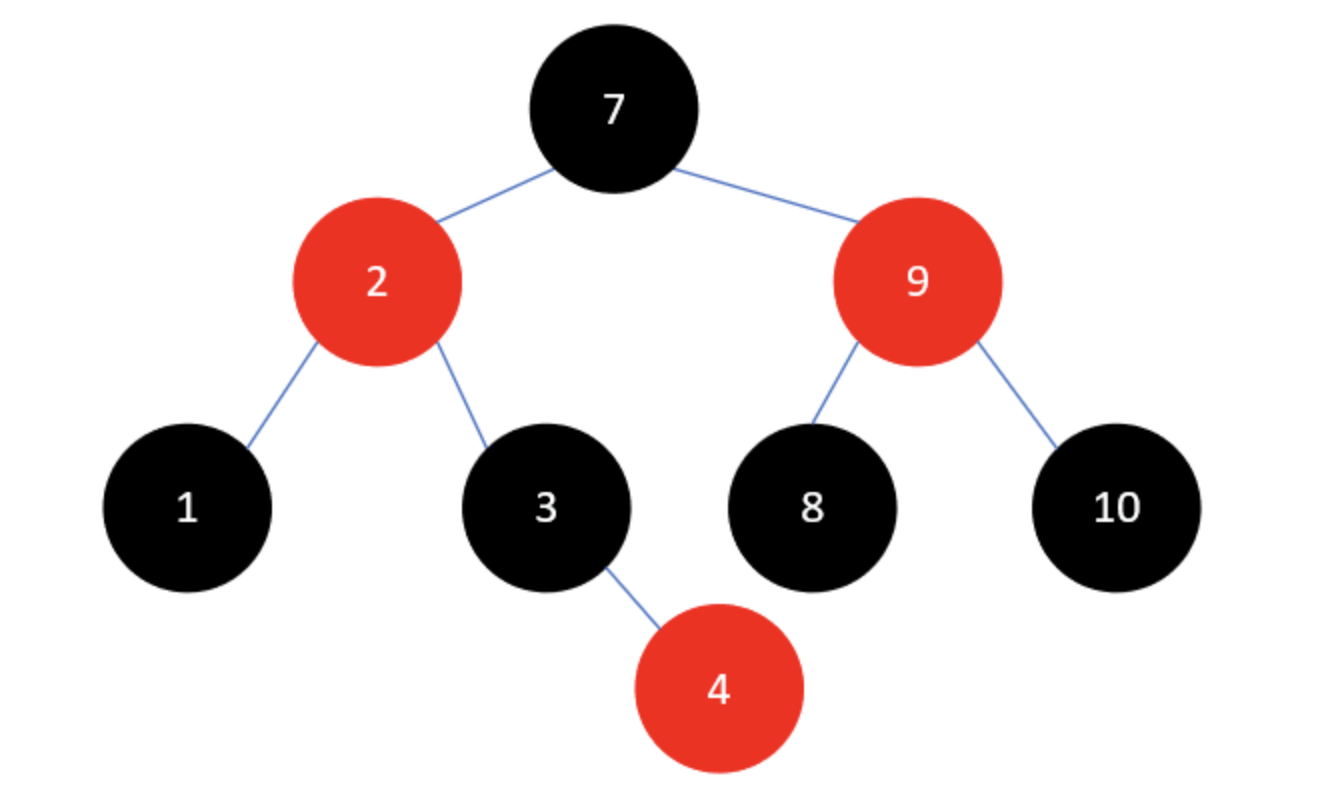
红黑树(Red-Black Tree,R-B Tree)
相对平衡的二叉查找树,不符合严格意义上的平衡二叉树
- 红黑树的节点一类被标记为黑色,另一类被标识为红色
- 根节点是黑色的
- 任何上下相邻的节点不能同时为红色,红色节点被黑色节点隔开
- 对于每个节点,从该节点到其叶子节点的所有路径,都包含相同数目的黑色节点
三、遍历方式

3.1 前序遍历
DLR,根-->左-->右。先访问根节点,然后遍历左子树,最后遍历右子树。
// 前序遍历:根节点 --> 左子树 --> 右子树
// 此函数接收根节点,并将遍历结果存储在数组res中
var preorderTraversal = function (root, res = []) {
// 如果当前节点为空,则直接返回,结束递归
if (!root) return [];
// 先访问根节点,将其值存入结果数组
res.push(root.val);
// 递归遍历左子树
preorderTraversal(root.left, res);
// 递归遍历右子树
preorderTraversal(root.right, res);
// 最终返回遍历结果
return res;
};
// root = [1,2,3,4,5,6,7];
preorderTraversal(root); //[1,2,4,5,3,6,7]
3.2 中序遍历
LDR ,左-->根-->右。先遍历左子树,再访问根节点,最后遍历右子树。
// 中序遍历:左子树 --> 根节点 --> 右子树
// 这个函数同样接收根节点,并收集遍历结果到数组res中
var inorderTraversal = function (root, res = []) {
// 当前节点为空,递归结束
if (!root) return [];
// 先递归遍历左子树
inorderTraversal(root.left, res);
// 然后访问当前根节点,将其值添加到结果数组
res.push(root.val);
// 最后递归遍历右子树
inorderTraversal(root.right, res);
// 返回遍历结果
return res;
};
// root = [1,2,3,4,5,6,7];
inorderTraversal(root); //[4,2,5,1,6,3,7]
3.3 后序遍历
LRD ,左-->右-->根。先遍历左子树,再遍历右子树,最后访问根节点。
// 后序遍历:左子树 --> 右子树 --> 根节点
// 此函数按照后序遍历的顺序收集节点值到res数组
var postorderTraversal = function (root, res = []) {
// 当前节点为空,直接返回
if (!root) return [];
// 先递归遍历左子树
postorderTraversal(root.left, res);
// 再递归遍历右子树
postorderTraversal(root.right, res);
// 最后访问当前节点,将其值加入结果数组
res.push(root.val);
// 返回最终的遍历结果
return res;
};
// root = [1,2,3,4,5,6,7];
postorderTraversal(root); //[4,5,2,6,7,3,1]
3.4 层序遍历
BFS,广度优先遍历。从上至下、从左至右逐层遍历节点。
// root = [1,2,3,4,5,6,7];
var levelOrder = function (root) {
let res = [];
function traversal(root, index) {
if (!root) return null;
if (!res[index]) res[index] = [];
res[index].push(root.val);
traversal(root.left, index + 1);
traversal(root.right, index + 1);
}
traversal(root, 0);
return res;
};
levelOrder(root); //[[1],[2,3],[4,5,6,7]]
四、练习题
4.1 二叉树的最大深度
递归地计算左右子树的深度,并返回左右子树中的较大深度值加 1(因为要加上当前层)
var maxDepth = function (root) {
if (root === null) return 0;
// 计算左子树的深度
let leftDepth = maxDepth(root.left);
// 计算右子树的深度
let rightDepth = maxDepth(root.right);
// 返回左右子树中深度较大的那一个加1(代表当前节点)
return Math.max(leftDepth, rightDepth) + 1;
};
4.2 二叉搜索树的最近公共祖先
- 二搜索树的节点的分布规则:左子树节点的值都小于根节点的值,右子树节点的值都大于根节点的值。
function lowestCommonAncestor(root, p, q) {
if (root.val > p.val && root.val > q.val) {
return lowestCommonAncestor(root.left, p, q);
}
if (root.val < p.val && root.val < q.val) {
return lowestCommonAncestor(root.right, p, q);
}
return root;
}
4.3 二叉搜索树的最小绝对差
- 二叉搜索树中序遍历后的节点是有序的,最小绝对差就是相邻两个节点之间的差值中的最小值。
- 在遍历过程中,记录上一个节点的值,并计算当前节点与上一个节点之间的差值,并更新最小绝对差。
var getMinimumDifference = function (root) {
let prev = null;
let minRes = Number.MAX_SAFE_INTEGER;
function inOrder(node) {
if (!node) return;
inOrder(node.left);
if (prev !== null) {
let abs = node.val - prev;
minRes = Math.min(minRes, abs);
}
prev = node.val;
inOrder(node.right);
}
inOrder(root);
return minRes;
};